Dongyeop Lee

2025

1. 

   SAFE: Finding Sparse and Flat Minima to Improve Pruning

   Dongyeop Lee, Kwanhee Lee, Jinseok Chung, and Namhoon Lee

   ICML 2025 (spotlight), Jul 2025

   Abs arXiv Code Poster

   Sparsifying neural networks often suffers from seemingly inevitable performance degradation, and it remains challenging to restore the original performance despite much recent progress. Motivated by recent studies in robust optimization, we aim to tackle this problem by finding subnetworks that are both sparse and flat at the same time. Specifically, we formulate pruning as a sparsity-constrained optimization problem where flatness is encouraged as an objective. We solve it explicitly via an augmented Lagrange dual approach and extend it further by proposing a generalized projection operation, resulting in novel pruning methods called SAFE and its extension, SAFE+. Extensive evaluations on standard image classification and language modeling tasks reveal that SAFE consistently yields sparse networks with improved generalization performance, which compares competitively to well-established baselines. In addition, SAFE demonstrates resilience to noisy data, making it well-suited for real-world conditions.

2. 

   SASSHA: Sharpness-aware Adaptive Second-order Optimization with Stable Hessian Approximation

   Dahun Shin*, Dongyeop Lee*, Jinseok Chung, and Namhoon Lee

   ICML 2025 (CKAIA 2024), Jul 2025

   Abs arXiv Code Poster

   Approximate second-order optimization methods often exhibit poorer generalization compared to first-order approaches. In this work, we look into this issue through the lens of the loss landscape and find that existing second-order methods tend to converge to sharper minima compared to SGD. In response, we propose Sassha, a novel second-order method designed to enhance generalization by explicitly reducing sharpness of the solution, while stabilizing the computation of approximate Hessians along the optimization trajectory. In fact, this sharpness minimization scheme is crafted also to accommodate lazy Hessian updates, so as to secure efficiency besides flatness. To validate its effectiveness, we conduct a wide range of standard deep learning experiments where Sassha demonstrates its outstanding generalization performance that is comparable to, and mostly better than, other methods. We provide a comprehensive set of analyses including convergence, robustness, stability, efficiency, and cost.

3. UAI

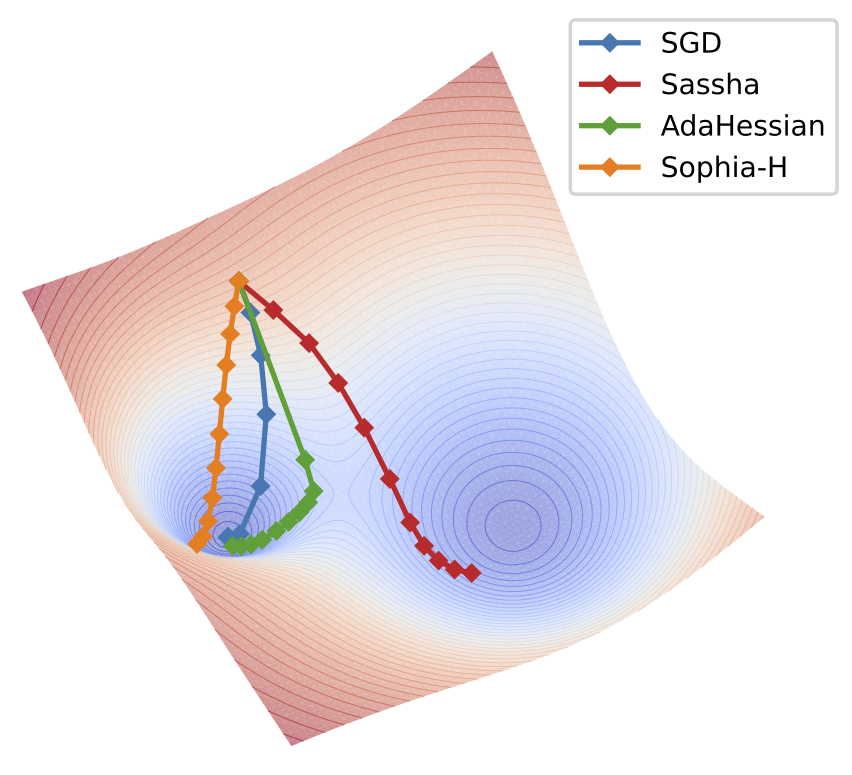
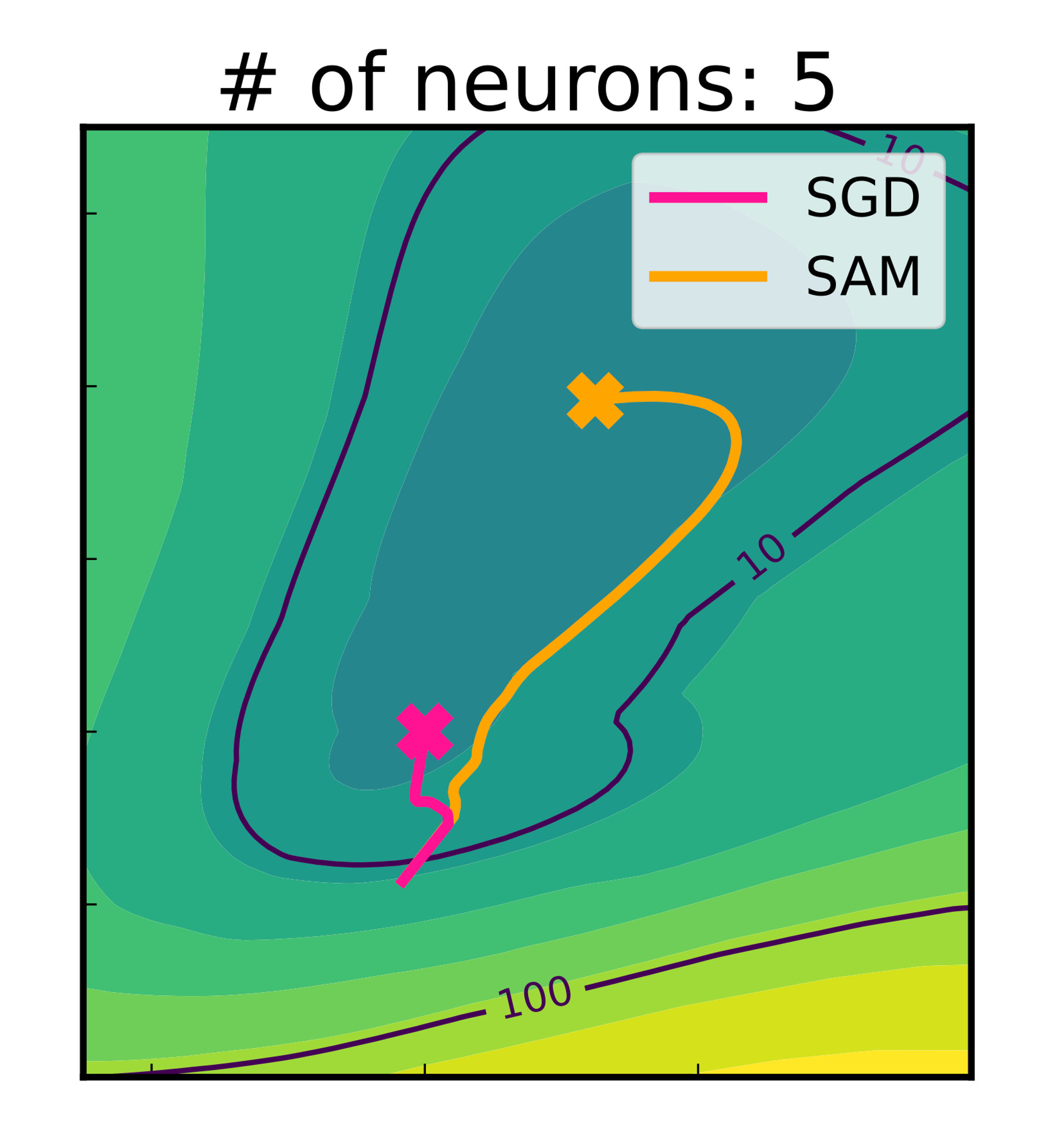
   Critical Influence of Overparameterization on Sharpness-aware Minimization

   Sungbin Shin*, Dongyeop Lee*, Maksym Andriushchenko, and Namhoon Lee

   UAI 2025 (ICML 2023 HiLD Workshop, Best paper award🏆@ JKAIA 2023), Jul 2025

   Abs arXiv Thread Code Poster

   Training an overparameterized neural network can yield minimizers of different generalization capabilities despite the same level of training loss. Meanwhile, with evidence that suggests a strong correlation between the sharpness of minima and their generalization errors, increasing efforts have been made to develop optimization methods to explicitly find flat minima as more generalizable solutions. Despite its contemporary relevance to overparameterization, however, this sharpness-aware minimization (SAM) strategy has not been studied much yet as to exactly how it is affected by overparameterization. Hence, in this work, we analyze SAM under overparameterization of varying degrees and present both empirical and theoretical results that indicate a critical influence of overparameterization on SAM. At first, we conduct extensive numerical experiments across vision, language, graph, and reinforcement learning domains and show that SAM consistently improves with overparameterization. Next, we attribute this phenomenon to the interplay between the enlarged solution space and increased implicit bias from overparameterization. Further, we prove multiple theoretical benefits of overparameterization for SAM to attain (i) minima with more uniform Hessian moments compared to SGD, (ii) much faster convergence at a linear rate, and (iii) lower test error for two-layer networks. Last but not least, we discover that the effect of overparameterization is more significantly pronounced in practical settings of label noise and sparsity, and yet, sufficient regularization is necessary.